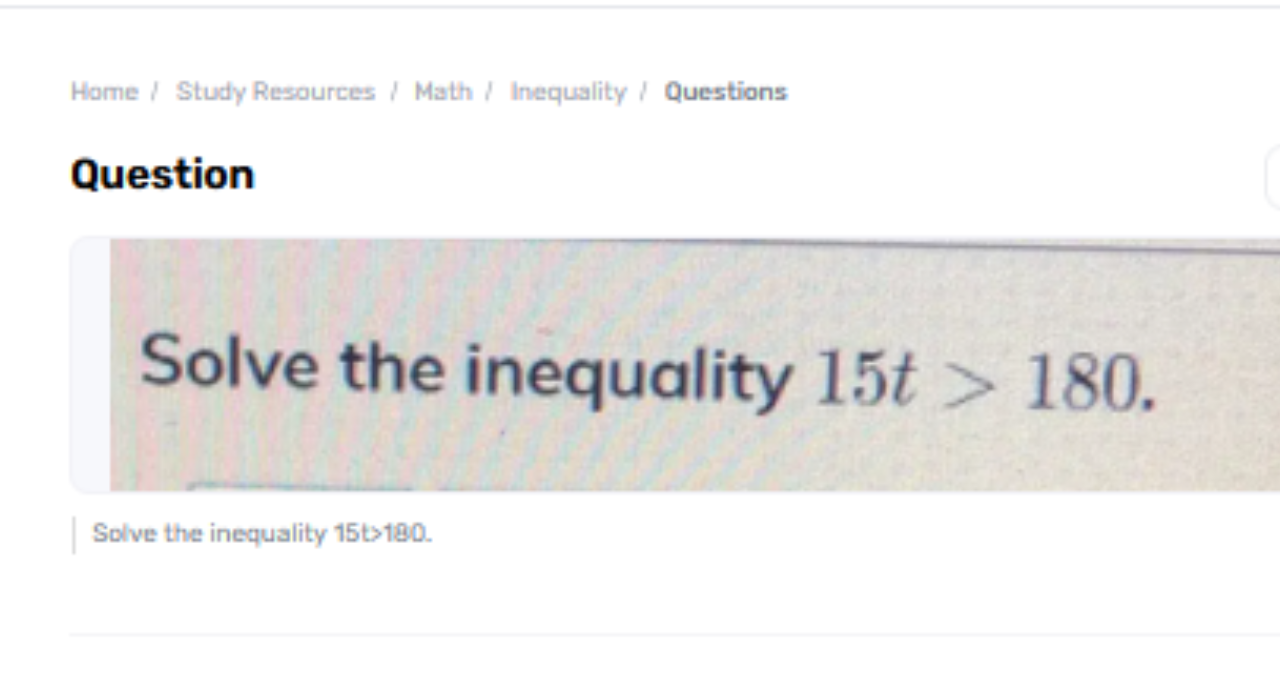
In science, disparities are utilized to portray an extent of values that a variable can take, instead of a single esteem. The inequality 15t>180 may be a direct imbalance including a variable ttt. To illuminate such imbalances, we ordinarily confine the variable on one side of the disparity sign. This preparation makes a difference in us deciding the set of values that fulfill the imbalance. In this clarification, we are going investigate how to unravel the imbalance 15t>180 step by step, give experiences into the arrangement, and examine the suggestions.
Tackling the Imbalance 15t>180
To fathom 15t>180, we confine it by separating both sides of the disparity by 15, coming about in t>12. This arrangement shows that it must be more noteworthy than 12 to fulfill the imbalance. Hence, any number more noteworthy than 12 may be a substantial arrangement.
Step-by-Step Arrangement
To unravel the disparity 15t>180, the primary step is to confine the variable it. This includes performing operations that simplify the inequality while keeping up its course. Here’s how it’s done:
1. Divide Both Sides by 15:
Since the coefficient within the disparity is 15, we have to partition both sides of the disparity by 15 to disconnect it. Partitioning both sides by a positive number does not alter the course of the disparity sign. Hence, we isolate:
15t15>18015frac{15t}{15} > frac{180}{15}1515t>15180
2. Simplify the Expression: Performing the division, we get:
t>18015t > frac{180}{15}t>15180
Calculating the right-hand side:
18015=12frac{180}{15} = 1215180=12
In this way, the disparity disentangles to:
t>12t > 12t>12
Translation of the Arrangement
The arrangement to the disparity 15t>18015t > 18015t>180 is t>12t > 12t>12. This implies that it can be any genuine number more prominent than 12. It does not incorporate 12 itself, but may be any number that's more prominent than 12. For occurrence, values like 13, 14, 20, or indeed 100 are all substantial arrangements to this disparity. In down-to-earth terms, this arrangement shows that if it speaks to an amount such as time, cash, or any quantifiable sum, it must surpass 12 units for the inequality to hold genuine.
Graphical Representation
Graphically, the arrangement t>12t > 12t>12 can be spoken to on a number line. On this number line, we put a circle at the number 12, which is open to show that 12 isn't included within the arrangement set. All numbers to the correct of 12 are shaded or checked to appear that they are included within the arrangement. This visual representation makes a difference in understanding the extent of values that fulfill the imbalance. The number line shows that the arrangement includes all numbers more prominent than 12.
Fundamental Steps for Utilizing the Gauth App to Yield an Address
Introduce and Make an Account
Secure the Gauth app from your app store and set up an unused client account.
Get to Your Account
Open the app and log in together with your account data.
Define Your Request
Enter your address into the given field and select an important category.
Yield Your Address
Tap the Submit button to send your inquiry for preparation.
Review Your Submission
Check the status of your question review any responses or updates provided by the app and give feedback.
Conclusion
In rundown, fathoming the disparity 15t>18015t > 18015t>180 includes segregating the variable ttt by partitioning both sides of the imbalance by 15, which leads to the streamlined shape t>12t > 12t>12. This result tells us that it must be more prominent than 12 to fulfill the imbalance. The translation and graphical representation assist in illustrating the arrangement, appearing that it can take on any value more prominent than 12. Understanding and tackling straight disparities like this is an essential aptitude in polynomial math, giving bits of knowledge into how factors are associated with given limitations.